Вода: микроструктура и флуктуации
С.Д. Захаров, М.В. Зюзин, И.В. Мосягина
Федеральное государственное бюджетное учреждение науки Физический институт имени П.Н.Лебедева Российской академии наук
Представлен краткий аналитический обзор экспериментов последних лет, относящихся к различным аспектам локальной организации воды. Исходным пунктом анализа является пространственное разделение воды на жидкость с нарушенными водородными связями и тетраэдрически координированные и флуктуирующие ассоциаты или кластеры размером 1-2 нм [1,2]. Показано, что кластеры могут существовать в двух различных формах, одной из которых является обычный гексагональный лед, тогда как основой другой служат модули, формирующие гидратные оболочки биомолекул. Кластеры осциллируют между двумя структурными состояниями, всякий раз испытывая переход «порядок-беспорядок». Асимметричные автоколебания, вероятно, имеют определенный ритм, не зависящий ни от температуры, ни от рН, но их амплитуда растет по мере охлаждения. Они являются источником флуктуаций различных физических параметров, характеризующих макроскопическое состояние воды, и активным агентом, синхронизующим биологические процессы.
Введение
Микроструктура жидкой воды традиционно рассматривается как в среднем однородное распределение молекул, стремящихся установить с ближайшими соседями водородные связи в направлении вершин правильного тетраэдра; при этом локальные неоднородности плотности, являющиеся результатом тепловых флуктуаций, должны, как обычно, увеличиваться с ростом температуры. Итоги выполненных недавно исследований, использовавших прецизионные рентгеновские методы, приводят к совершенно другой картине: вода представляет собой смесь двух жидкостей с различной локальной организацией. В одной из них водородные связи частично нарушены, тогда как другая представляет собой флуктуирующие тетраэдрически координированные наноразмерные ассоциаты, и такая картина сохраняется вплоть до кипения [1,2]. При этом флуктуации с понижением температуры не ослабляются, а, напротив, растут.
Нарастание флуктуаций, только гораздо резче выраженное, было обнаружено ранее по мере переохлаждения воды вплоть до -26 оС [3]. Для объяснения этого факта было выдвинуто несколько гипотез, и одна из них, о существовании у воды двух структурных модификаций, наличия между фазового перехода I рода «жидкость-жидкость» и близости (на фазовой диаграмме) соответствующей (второй) критической точки и критических флуктуаций [4], получила наибольшую популярность. Отметим, что авторы [1] интерпретировали свои результаты как подтверждение этой гипотезы.
Такая объяснение признается не всеми [5], и проблема активно дебатируется. Ее решение имеет огромную важность, так как позволило бы понять причину многих странностей воды. Однако на этом пути предстоит еще немало сделать: в частности, авторы работы [1] подчеркнули, что детальная организация флуктуирующих локальных структур и временные масштабы ими не определены. Настоящая статья представляет собой, насколько нам известно, первую попытку найти подход к решению этих задач. Выбор экспериментальных данных, которые приняты во внимание, конечно, ограничен и субъективен, что до некоторой степени компенсируется охватом нескольких областей исследований. Мы включили лишь основные результаты, касающиеся изучения динамики переохлажденной воды, организации гидратных оболочек биомолекул, природы клеточных ритмов.
За кратким обзором следует оригинальная часть. Здесь аргументировано, что тетраэдрическая координация в нанокластерах, обнаруженная в работе [1], может быть реализована не единственным способом, т.е. на базе решетки гексагонального льда Ih, а двумя. Структурной основой ассоциатов второго типа служит модульная организация упорядоченной части (каркаса) гидратных оболочек биополимеров [6]. Вероятность формирования нанокластеров обоих типов примерно одинакова, благодаря чему они могут присутствовать в воде одновременно, следовательно, конкурировать друг с другом. Это должно приводить к возникновению осцилляций между двумя типами структур, которые становятся источником флуктуаций термодинамических параметров. С понижением температуры средний размер кластеров увеличивается, и амплитуда флуктуаций, в согласии с наблюдениями, возрастает. Кооперативность межмолекулярных взаимодействий приводит к тому, что вместо одного характерного временного масштаба осцилляций имеется иерархия времен. Ритм воды коррелирует с колебаниями относительного содержания орто/пара спин-изомеров Н2О вокруг равновесного отношения 3:1 и потому не зависит ни от температуры, ни от рН.
I. Обзор экспериментальных данных
1.1. Переохлажденная вода
Вода, подобно другим жидкостям, может быть переохлаждена посредством медленного отбора тепла [8]. Явление переохлаждения распространено в природе (капли в облаках, стадия жизни земноводных) и используется для консервации клеток [9]. В лабораторных условиях минимальные температуры, еще совместимые с жидким состоянием, достигаются тщательным удалением растворенных и взвешенных примесей. (Возможность загрязнения логарифмически уменьшается с уменьшением размера образца, поэтому в большинстве работ по переохлаждению используются образцы очищенной воды очень малого объема).
Даже при выполнении этого требования предел переохлаждению ставит внезапное гомогенное зародышеобразование, превращающее весь объем образца в ледяной монолит; при атмосферном давлении оно наступает при ТН = 231 К (-42 оС) [10].
Охлаждая воду быстро, скажем, при 106 К/с, до 77 К (температура жидкого азота), получают стекловидную форму, называемую аморфным льдом низкой плотности (АЛНП) [11]. Приложение давления 11000 атм к льду Ih, охлажденному до 77 К, приводит к образованию более плотной (на ~25%) формы водяного стекла, аморфного льда высокой плотности (АЛВП) [12]; при определенных условиях обе аморфных модификации взаимно превращаемы [13]. Полагают, что жидкая вода также имеет две формы, соответственно, низкой плотности (НЖ) и высокой плотности (ВЖ). [14, 15]. Тогда вполне мыслимо существование перехода между двумя видами воды. Если зона перехода на фазовой (Р,Т) диаграмме не слишком далека от окружающих (нормальных) условий, то «отголоски» критического поведения будут отзываться на свойствах обычной воды, что даст ключ к разгадке ее странностей. Так как детали фазовой диаграммы воды при низких температурах практически неизвестны, фронт исследований в этом направлении, несмотря на огромные трудности, расширяется [16].
По мере охлаждения воды ее функции отклика, такие
как теплоемкость при постоянном давлении СР = Т(![]() )Р,
изотермическая сжимаемость
)Р,
изотермическая сжимаемость ![]() , коэффициент теплового расширения
, коэффициент теплового расширения ![]() , где S –
энтропия, r - плотность, ведут себя
необычно. Достигнув некоторого минимума, они начинают расти, причем тем круче,
чем температура меньше; рост удалось пока проследить до 247 К (-26 оС)
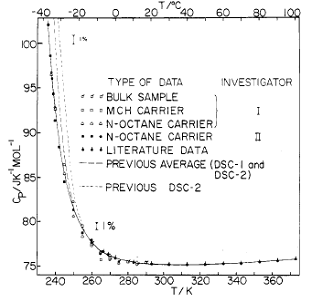
[3] (Рис. 1). При экстраполяции дальнейшего хода кривых обнаруживается их
тенденция к расходимости при одной и той же температуре Тs = 228 К (-45 оС), недоступной из-за
ранее наступающей однородной кристаллизации при -42 оС [17].
, где S –
энтропия, r - плотность, ведут себя
необычно. Достигнув некоторого минимума, они начинают расти, причем тем круче,
чем температура меньше; рост удалось пока проследить до 247 К (-26 оС)
[3] (Рис. 1). При экстраполяции дальнейшего хода кривых обнаруживается их
тенденция к расходимости при одной и той же температуре Тs = 228 К (-45 оС), недоступной из-за
ранее наступающей однородной кристаллизации при -42 оС [17].
|
|
|
|
а |
б |
|
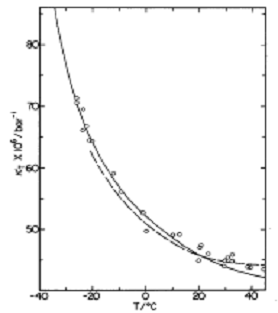
Рис. 1. Теплоемкость (а) и изотермическая сжимаемость (б) воды в переохлажденном режиме резко растет (C. A. Angell et al. J. Chem Phys., 86, 998 (1982; [3]) |
|
С другой стороны, функции отклика пропорциональны соответствующим
флуктуациям, а именно ![]() ,
, ![]() ,
, ![]() [18]. Отсюда вытекает важный вывод: с
приближением к температуре Тs
в водном объеме нарастают флуктуации плотности и энтропии. Такое поведение
можно объяснить влиянием фазового перехода 1 рода между упомянутыми выше
жидкостями с двумя различными структурами [4]. (Отметим, что выдвинуты и другие
гипотезы, см. ссылки в [19]). Тогда при более высоких значениях температуры и давления
преобладает ВЖ, а при более низких - НЖ. Точка на Р,Т диаграмме,
где обе жидкости перестают различаться, названа второй критической точкой. Если
известной («первой») критической точке жидкость-пар соответствуют Т = 374 °C и Р = 218 атм., то эта гипотетическая точка лежит в области, недоступной для эксперимента (Т~
220 К, Р~ 1000 атм). Отметим, что поиски перехода «жидкость – жидкость» в других
системах, стимулированные данной гипотезой, увенчались успехом: подобный переход
найден в кремнии [20].
[18]. Отсюда вытекает важный вывод: с
приближением к температуре Тs
в водном объеме нарастают флуктуации плотности и энтропии. Такое поведение
можно объяснить влиянием фазового перехода 1 рода между упомянутыми выше
жидкостями с двумя различными структурами [4]. (Отметим, что выдвинуты и другие
гипотезы, см. ссылки в [19]). Тогда при более высоких значениях температуры и давления
преобладает ВЖ, а при более низких - НЖ. Точка на Р,Т диаграмме,
где обе жидкости перестают различаться, названа второй критической точкой. Если
известной («первой») критической точке жидкость-пар соответствуют Т = 374 °C и Р = 218 атм., то эта гипотетическая точка лежит в области, недоступной для эксперимента (Т~
220 К, Р~ 1000 атм). Отметим, что поиски перехода «жидкость – жидкость» в других
системах, стимулированные данной гипотезой, увенчались успехом: подобный переход
найден в кремнии [20].
Нарастание флуктуаций по мере переохлаждения однозначно интерпретировать не удается. Согласно наиболее авторитетной гипотезе, точка на фазовой диаграмме с уменьшением температуры приближается к особой линии максимумов корреляционной длины, которая исходит из критической точки (линия Видома). Нельзя также исключить, что происходит сближение с границей абсолютной неустойчивости одной из фаз (спинодалью) [21]. Переход системы через линию Видома непрерывный и потому сопровождается прохождением функций отклика через экстремумы; напротив, при переходе через спинодаль они изменяются скачком. В первом случае вода является структурно однородной жидкостью с гомогенными, по терминологии Френкеля, флуктуациями плотности. [22]. В последнем случае, флуктуации гетерогенны, т.е. неоднородности плотности являются островками другой фазы. Чтобы проверить непосредственно, какой из сценариев верен, необходимо переохладить воду до -45 оС, но эта температура находится уже за границей неизбежной кристаллизации.
1.2. Обладают ли гидратные оболочки белков структурой?
Микроструктура воды должна отражаться на динамическом сцеплении воды и биомолекул, и хотя последнее еще мало изучено, но уже признано критичным для биологического действия [23,24]. Исследования непосредственно в растворе пока чрезвычайно трудны и недостаточно информативны. Для этих целей, как правило, применяют методы малоуглового нейтронного и рентгеновского рассеяния [25], а также фемтосекундной спектроскопии [26]. Толщина гидратной оболочки ДНК и ряда белков в растворе, определенная с помощью люминесцентного зонда, возбуждаемого фемтосекундными лазерными импульсами, составляет примерно 7 Ǻ, тогда как резидентное время молекулы воды имеет два значения ~1 и 20-40 ps [26].
Более просто получить количественные данные для белковых кристаллов, где эффективны методы нейтронной дифракции [27] в комбинации с рентгеновской дифракцией. В частности, определено положение » 300 молекул Н2О в окружении белка трипсина [28]. При этом обнаружено несколько устойчивых конфигураций молекул Н2О, сохраняющих положение даже в родственном белке трипсиногене. Показано также, что более 70% молекул в первом гидратном слое трипсина обладают структурным порядком, представляя собой кластеры из сетей, связанных водородными связями, причем многие из них локализуются вдоль контактов между макромолекулами [29]. Подчеркивается, что структура ряда областей трипсина представляет собой более упорядоченную картину, если ее характеризовать конфигурацией молекул воды, а не атомов белка.
Поскольку по мере охлаждения молекулярное движение замедляется, дифракционная картина криокристалла в рентгеновских лучах приобретает большую четкость, и в структуре водного окружения белка отчетливо проявляется определенный порядок [30]. Молекулы Н2О, благодаря склонности к тетраэдрической координации, образуют трехмерные цепочечные соединения между гидратной оболочкой и полярными атомами белка. Сеточки водородных связей, покрывающие всю поверхность белка, достаточно гибки, чтобы обеспечить конформационные изменения и существенно влиять на его динамику и функции.
В активном центре глутомат дегидрогеназы выявлены, с помощью рентгеноструктурного анализа и малоуглового рентгеновского рассеяния, крупно-масштабные смещения доменов третичной структуры, сопряженные с изменениями гидратационной структуры [31]. При этом определена локализация 1931 молекул Н2О, окружающих данный фермент.
Недавно представлены некоторые детали структурного порядка в водном окружении полутора тысяч белковых кристаллов из доступной исследователям базы данных [32]. В гидратных оболочках обнаружено множество полигональных водных структур, содержащих от 3 до 8 молекул. Предполагается, что эти многоугольники представляют собой усредненные по времени и пространству структуры «стабильных» водных олигомеров, которые присутствуют в обычной жидкой воде и существенны для понимания ее физических свойств.
1.3. Кристаллографический подход
Из вышеописанных отрывочных сведений о гидратных оболочках можно сделать вывод, что, они, по-видимому, включают в себя две подсистемы. Одна из них, сформированная водородными связями с полярными остатками, имеет низкую плотность с признаками порядка, тогда как в другой, более плотной, эти признаки не обнаружены. Общие закономерности построения упорядоченной подсистемы или каркаса найдены методами кристаллофизики [6]. Водный каркас строится из универсальных модулей, обладающих свойством фрактального масштабирования; он комплементарен периферийной структуре биомолекулы, что подтверждено прямой демонстрацией на моделях ДНК, белка коллагена и ряда других биополимеров.
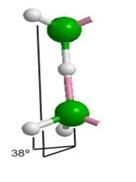
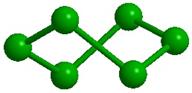
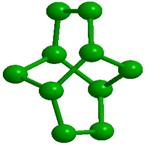
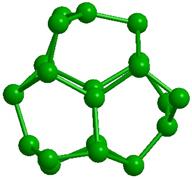
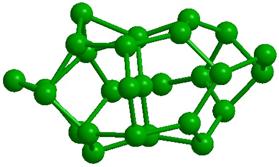
Образованию подобных модульных структур благоприятствует способность молекул Н2О деформироваться, сохраняя тетраэдрический характер координации. Водный димер при определенном значении угла скрученности (около 38о) вокруг общей связи образует при двойниковании кольцо из 6 молекул (гексамер) со структурой «твист-ванна»; такие гексамеры входят в структуры более высокого уровня (модули, размер менее 1 нм), обладающие свойством фрактальности (рис. 2). Из них составляются спиральные цепочки, плоские и изогнутые полосы, сверхрешетки и даже замкнутые оболочки [33]. Полярные группы биополимера и донорно-акцепторные Н-связи молекул воды объединяются в единую конструкцию и совместно поддерживают её устойчивость. Происходящий при этом проигрыш в энтропии компенсируется энтальпийным выигрышем. Небольшая энергия водородной связи допускает, в случае изменении внешних условий, быструю перестройку интерфейса, обеспечивая необходимую для живого лабильность.
|
|
|
|
|
|
a |
б |
в |
|
|
|
|
||
|
|
|
||
|
г |
д |
||
|
Рис. 2. Иерархия модулей «фрактального» льда: а -димер, б - гексацикл (Н2О)6 или твист-ванна, в - (Н2О)10 или th-цикл, г - (Н2О)20 или L-кластер, д -(Н2О)27 или Т-кластер. В структурах с n> 2 показаны только атомы кислорода, а для г и д приведены два вида – сбоку и сверху. |
|||
Участие упорядоченных гидратных оболочек подозревается в явлении, называемом светокислородным эффектом [34, 35]. Красные клетки крови в определенных температурных интервалах оказываются окруженными протяженной зоной с пониженным показателем преломления, исчезающей при фотовозбуждении молекул растворенного кислорода на синглетные электронные уровни. При этом деформируемость эритроцитов значительно повышается. Расчеты показывают, что менее плотная зона пронизана нитевидными льдоподобными образованиями, вырастающими на специфических сайтах (гликопротеины?) клеточной мембраны.
1.4. Биоритмы и флуктуации
Вывод о росте флуктуаций при переходе в режим глубокого переохлаждения получен как следствие нелинейного увеличения функций термодинамического отклика; при этом ни об амплитуде, ни о спектре флуктуаций никаких данных нет, т.к. в равновесной термодинамике временные параметры не играют роли. Все же прямая информация о них может оказаться очень полезной, тем более, что за два десятилетия ни одна из гипотез относительно структуры воды не добилась реального перевеса. Такая возможность открывается, если учесть один из результатов цитированной выше работы [1]: флуктуации в подсистеме тетраэдрически координированных кластеров сохраняются во всем температурном интервале стабильности воды вплоть до кипения. В таком случае можно обратиться к другим исследованиям, большая часть которых выполнена в обычных условиях.
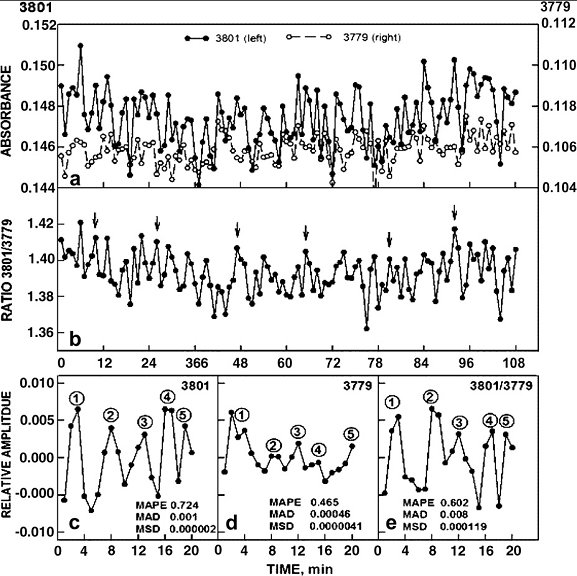
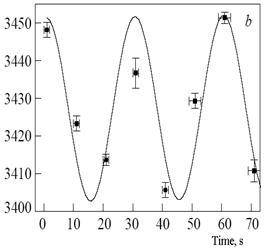
J. и D. Morre из университета Purdue (USA) обнаружили, что клетки в течение ~12 мин растут, следом на ~12 мин их рост прекращается, затем цикл повторяется [36]. Ответственный за ритм белок (ENOX) был ими выделен; оказалось, что этот фермент СuII-зависим, может функционировать в растворе, имеет двойную активность, а его средний период (24 мин), выделенный из временного ряда быстрых осцилляций, состоит из пяти неэквидистантных (2+3) максимумов и не зависит ни от температуры, ни от pH. Действуя методом последовательных исключений, авторы показали, что (2+3) структура сохраняется на всех этапах; источником ритма является сама вода, а именно, квазипериодические колебания орто/пара отношения ее ядерных спин-изомеров (в чистой воде период равен ~18 мин) [37] (рис.3).
|
|
|
Рис. 3. Осцилляции орто- и пара- спин-изомеров Н2О, наблюдаемые по интенсивности вращательно-колебательных линий в Фурье-спектре в парах вблизи водной поверхности [37]. |
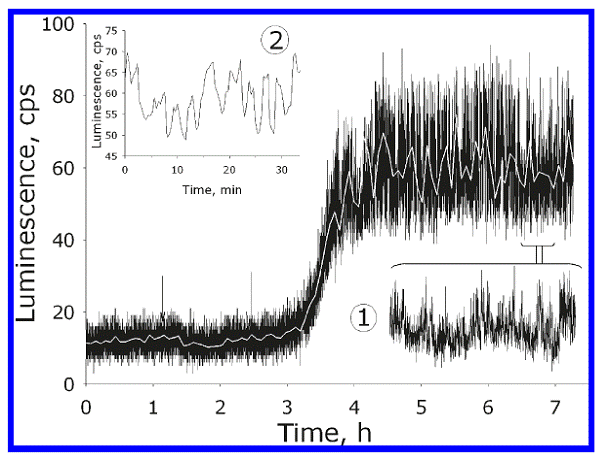
Вода при комнатной температуре люминесцирует слабо (~1 фотон мл-1.с-1) в сине-зеленой области в результате рекомбинации термически возбуждаемых радикалов, а также под влиянием естественной радиоактивности и космических частиц [38]. Люминесценцию можно повысить на полтора порядка и, что особенно интересно, перевести в режим автоколебаний [39]. Для этого достаточно в течение нескольких минут проэкспонировать образец воды к лазерному лучу с длиной волны 1,264 мкм, которая соответствует электронному переходу в молекулах растворенного кислорода 3Σg→ 1Δg. За это время в пробирке образуется (и исчезает) небольшое количество молекулярного синглетного кислорода, который обладает малым временем жизни (3-4 мкс). После некоторого периода задержки, достигающего полутора часов, интенсивность люминесценции начинает возрастать, и устанавливаются автоколебания, которые продолжаются около суток (светокислородный эффект в чистой воде). Деоксигенация воды или выведение длины волны из полосы поглощения О2 приводят к исчезновению явления, свидетельствуя, что запуск процесса производится именно синглетным кислородом. Вейвлет-анализ временных рядов, полученных при регистрации люминесценции, выявляет два характерных периода пульсаций 300 и 1150 с (рис. 4). Последний из них практически совпадает с периодом 18 мин, обнаруженным в работе [37], цитированной выше. Молекула О2 парамагнитна, ее электронный спин S=1, но в синглетном состоянии S=0. Предполагается, что переключение электронных спинов индуцирует накопление в воде радикалов и синхронизует рекомбинационный ритм [40].
|
|
|
Рис. 4. Возникновение автоколебаний люминесценции при действии на воду лазерного излучения в полосе поглощения растворенного кислорода. Вода была экспонирована в течение 5 мин (момент указан стрелкой) к ИК излучению (λ = 1264 nm, мощность 5 mW). До стрелки регистрируется фоновая люминесценция до начала облучения. Белая линия на основном графике представляет сигнал после сглаживания. Вставка 1 и 2 показывают участок с высоким временным разрешением и отвечающую ему интегральную интенсивность соответственно [37]. |
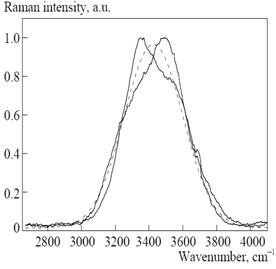
Для изучения динамики водных систем успешно применяются методы четырехфотонного рамановского рассеяния. С помощью этих методов обнаружены квазипериодические колебания центра спектральной полосы, которая соответствует моде растяжения ОН связи в Н2О. В спектрах дистиллята обнаружены квазипериодические (20-50 с) осцилляции центра колебательной полосы растяжения валентной О-Н связи молекулы Н2О [41] (рис. 5). Подозревается, что это колебания вокруг состояния равновесия двух коллективных структур воды с «сильными» (пара-вода) и «слабыми» (орто-вода) водородными связями.
|
|
|
|
Рис. 5. Осцилляции центра колебательной полосы растяжения валентной О-Н связи молекулы Н2О в жидкой воде при комнатной температуре [41 ]. |
|
II. Результаты и обсуждение
2.1. Методы
Моделирование водных структур производилось в пакете программ BioChemOffice и HyperChem8. Построенные в этих программах структуры затем корректировались для согласования с известными экспериментальными данными. Для определения параметров стыковки частиц с тетраэдрическими связями использовался пакет AutoCad 2009.
2.2. Флуктуации: сравнительный анализ
Сопоставим между собой два экспериментальных результата, полученных в разных областях исследований и связанных с флуктуациями в водном объеме. С одной стороны, в воде присутствуют наноразмерные кластеры с тетраэдрической координацией, характерной особенностью которых является их неустойчивость (см. Введение). С другой стороны, в переохлажденной воде нарастают флуктуации плотности (и энтропии) (п. 1.1). Так как в обоих случаях речь идет о флуктуациях одной и той же величины – локального объема (и локального порядка), логично заключить, что источник у них один и тот же. Чередование разрушения и самосборки кластеров приводят к локальным флуктуациям плотности, наблюдаемым с помощью малоуглового рентгеновского рассеяния, и они увеличиваются с уменьшением температуры в согласии с данными термодинамики. Следовательно, частотно-амплитудный спектр термодинамических флуктуаций является некоторым нелинейным преобразованием спектра кластерных флуктуаций.
Теперь возникает вопрос об осцилляциях орто-пара отношения, задающих клеточный ритм: можно ли считать их независимыми от термодинамических флуктуаций? Априори такая возможность не исключена, но маловероятна. Динамика спиновых степеней свободы отражается на внутримолекулярном движении через спин-орбитальное сцепление, а изменения внутри молекул влияют на межмолекулярные взаимодействия. Временной паттерн орто-пара осцилляций (2+3 неэквидистантных максимума) повторяется во временной структуре колебаний клеточного роста, конформационных подвижек в ферменте, деформаций гидратной оболочки иона (п. 1.4), тогда как «большой» период (18 мин) согласуется с ритмом (1150 с) автоколебаний собственной люминесценции воды, запускаемой СКЭ (п.1.5). Эти совпадения дают веские основания для заключения о единой природе спектров. Флуктуации объема и энтропии определяют термодинамические функции отклика. Они представляют ритм воды, которому теперь можно приписать свойства, обнаруженные для орто-пара осцилляций, а именно независимость частотных характеристик (но не амплитуд) от температуры и рН. Можно предположить, что этот универсальный ритм находится в близком соответствии с ритмом низкочастотных флуктуаций, коррелированных с космофизическими факторами (С.Э. Шноль) [42].
2.3. Альтернатива гексагональному льду
Таким образом, вероятными источниками флуктуаций в стабильной и переохлажденной фазе являются образование и распад кластеров. Необходимо понять причину их нестабильности, что невозможно без знания как они устроены. Вопреки общепринятой точке зрения, это не обязательно структура гексагонального льда, если принять во внимание принципиальный вывод. рентгеновского зондирования: присутствие кластеров во всем температурном диапазоне стабильности воды вплоть до кипения Тb. Легко представить, что при таянии льда в жидкую фазу переходят, - и в течение некоторого времени там существуют - агрегаты из нескольких и даже десятков молекул, сохраняющих остатки решетки Ih. (Оставляем в стороне пресловутую проблему особых свойств талой воды). Однако присутствие льдоподобных частиц вблизи точки фазового перехода жидкость-пар (373 К), где начинается интенсивный рост зародышей газовой фазы, маловероятно (если, конечно, не вмешиваются благоприятствующие процессы!).
Казалось бы, теперь нет иного выхода, как присоединиться к господствующей интерпретации, рассматривающей кластеры как неоднородности плотности, возникающие благодаря влиянию второй критической точки Тс2 [4]. Эта концепция, однако, сталкивается с проблемой, на которую указал C.A. Angell: находится ли эта гипотетическая точка на (Р,Т) диаграмме в достаточной близости к области измерений, чтобы приближением к ней объяснить обнаруженные флуктуации? [43]. Известно, что температурный диапазон, на который распространяется влияние критических явлений, зависит от характера действия межмолекулярных сил [44]. Если силы убывают с расстоянием достаточно быстро, напр., r-6 в случае сил ван-дер-Ваальса в обычных жидкостях, то флуктуации сильные, и критические явления обнаруживаются задолго до приближения к Тс, когда безразмерная температура q = (Т - Тс)/Тс ~1. Напротив, если молекулы взаимодействуют на значительных расстояниях, что характерно для кулоновских и диполь-дипольных взаимодействий, то установившееся в среде силовое поле почти не искажается флуктуациями вплоть до непосредственной близости к Тс, где q ~ 10-3. Вода с ее распространенными водородными связями скорее принадлежит ко второму типу. Даже для переохлажденной жидкости при Т = 250 К и Тс » 220 К значение q = 0,13, а для Тb = 373 К получим q = 0,7. Это на два-три порядка шире границы диапазона, ожидаемого для сценария с приближением к линии Видома (см. п. 1.1.).
Вернемся к идее о кластерах как зародышах новой фазы, и обсудим, не являются ли ими элементы упорядоченных гидратных оболочек, присущие биомолекулам в растворах (см. п.1.3)? Для структур такого типа - будем называть их ниже для краткости акванами (Aq) - характерна тетраэдрическая координация, и это свойство уже делает их подходящими кандидатами. Конечно, в отличие от кристаллической фазы, акванами невозможно «замостить» все пространство, поэтому они, в классическом смысле, не представляют собственно фазу, но в данном случае этого и не требуется: на масштабах ~ 1 нм они могут быть довольно компактными образованиями.
Возникают ли акваны в объемной воде вдали от биомолекул? На этот вопрос прямого ответа нет. Разработка и применение метода седиментационной рефрактометрии в исследованиях СКЭ позволили получить определенные указания на такую возможность [35]. По этим данным, прилегающая к мембране эритроцита область протяженностью 5-10 мкм представляет собой гидрогель - водный раствор, пронизанный сеткой льдоподобных наноразмерных (по толщине) волокон. На внешней стороне мембраны, вероятно, имеются белки, конфигурация периферии которых «способна имитировать фрагмент грани льдоподобной кристаллической решетки (но не Ih!). В таком случае на них, как на зародышах соответствующей фазы могут наращиваться, а затем, возможно, объединяться в сеть, динамические структуры из молекул Н2О [35]»
В другом, столь же важном аспекте проблемы – могут ли акваны возникать при повышенных температурах – также нет достаточной ясности. Косвенную поддержку этому предположению дают факты существования жизни в горячих источниках (термофильные бактерии). Отсюда, по крайней мере, можно заключить, что в комплексе с биомолекулами, гидратные оболочки, а с ними акваны, существуют вблизи точки кипения. Далее будет предположено, что акваны могут на короткое время образовываться спонтанно в водных объемах. Рассмотрим их возможную организацию и оценим вероятность образования по отношению к кластерам на основе решетки Ih.
2.4. Кластеры со структурой модульного типа
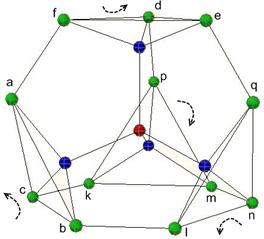
Исходными «кирпичиками», из которых строятся акваны, являются универсальные блоки (модули) (Н2О)n, n = 2, 6, 10, 20, 27 с размерами не более 1 нм, обладающие свойством хиральности, что позволяет создавать из них спирали, трубки, плоские и искривленные слои и т.п. [4, 5]. На рис. 2 видно, как из двух мономеров, повернутых вокруг общей водородной связи, образуются димеры, затем гексамеры, которые входят во все последующие структуры более высокого уровня. Хотя эти структуры описаны давно, нам не удалось найти первоисточник, в котором обосновывается особое значение параметра стыковки (38o) двух молекул воды (в исходной работе [4] приводится идея доказательства, результирующий график и ссылка на отчет японского автора, но поиск среди опубликованных изданий и в сети не дал результатов). Параметром стыковки тетраэдрических частиц, атомов или молекул мы называем торсионный угол Θ или угол скручивания двух частиц по линии общей связи (рис.6). Для кристаллических структур типа вирцита (лёд 1h) и лонсдейлита (лёд 1с) Θ = 0° и 60° соответственно.
Оказывается, что кроме этих двух известных значений имеется ранее незамеченный узкий диапазон углов, позволяющий создавать фрактальные структуры из некоторых универсальных блоков или модулей. Соответствующее значение параметра Θ @ 38о может быть определено аналитически на модели кластера из 17 атомов (полиэдр Лавеса) (рис. 6). Этот кластер был образован по следующему принципу. К центральному атому по тетраэдрическим направлениям были присоединены четыре атома, образующие первую координационную сферу. Затем к этим четырем атомам по трем оставшимся у каждого атома связям были присоединены ещё двенадцать атомов, которые образуют вторую координационную сферу. Данное положение соответствует Θ=0°. При синхронном повороте всех четырех троек атомов в одном и том же направлении и с одинаковым угловым шагом расстояния одной фиксированной вершины кластера до одиннадцати других его вершин изменяются. Мы выполнили эти расчеты, и результаты показаны на рис. 6; в пределах от 0 до 60о они совпадают с графиком из [4].
|
|
|
|
|
|
|
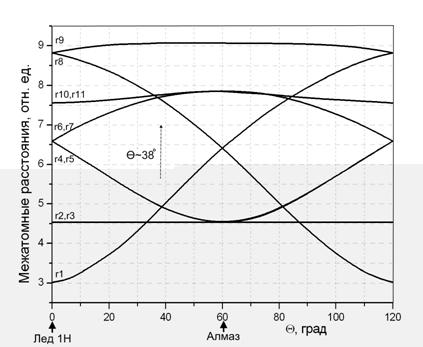
Рис. 6. К определению параметра стыковки Q (380) тетраэдрических координированных частиц, позволяющего образовывать из молекул воды модули, показанные на рис. 1. Изменение расстояний в полиэдре Лавеса при синхронном повороте четырех троек атомов в одном направлении в разных плоскостях. r1=af, r2=ab, r3=ac, r4=ad, r5=ae, r6=ak, r7=al, r8=am, r9=an, r10=ap, r11=aq. |
|
При значении Θ около 38° расходящиеся кривые сближаются, что
соответствует образованию во второй координационной сфере икосаэдра с тремя
наборами эквивалентных расстояний {r1(ab
,ac ,ad ,ae
,af), r2(ak,
al, am, an,
ap) и r3=aq}
(архимедов кубоктаэдр, соответствует параметру Θ=60° и фрагменту структуры
алмаза). Таким образом, при сборке тетраэдрического кластера вторая
координационная сфера может быть образована тремя способами (Θ=0°, 38°,
60°), так как только в этом случае в ней формируются симметричные многогранники,
обеспечивающие связанность структуры.
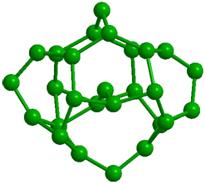
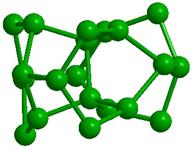
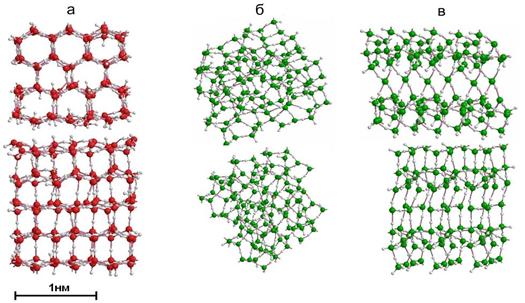
Водные кластеры воды моделировались нами следующим образом. К свободным связям исходного элементарного модуля присоединялись свободные связи другого блока и т.д. вплоть до достижения требуемого числа молекул и размеров. Поскольку такое построение не может быть однозначным, на рис. 7б,в представлены два варианта, один из которых напоминает сферу, а другой кубик. Там же (рис. 7а) показан кластер со структурой гексагонального льда. Размеры всех льдоподобных фрагментов около 1,3 нм, что соответствует размерам неоднородностей низкой плотности, указанным в работе [1].
|
|
|
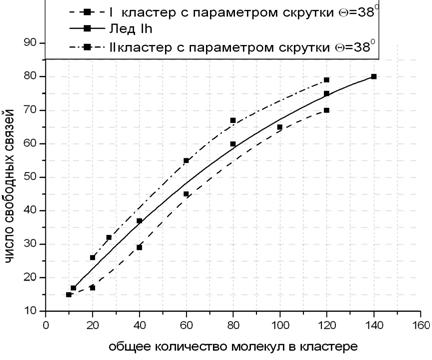
Рис. 7. Модели водных кластеров в двух ортогональных проекциях: а) на основе решетки льда Ih, количество молекул N=140; б) из (Н2О)20 модулей, N=120 (кластер I); из (Н2О)10 модулей, N=120 (кластер II). |
Чтобы корректно судить о том, какой из кластерных типов может существовать в жидкой воде, необходимо вычислить свободную энергию для различных форм. Нами использована упрощенная процедура: по мере увеличения размера кластера подсчитывается число свободных (водородных) связей, что примерно соответствует поверхностной энергии. Согласно принятому критерию, меньшее число таких связей в расчете на одну молекулу, при прочих равных условиях, отвечает более устойчивой конфигурации кластера. Результаты таких тестов для структур, показанных на рис. 7, представлены на рис. 8.
|
|
|
Рис.8. Зависимость числа свободных связей от числа молекул по мере увеличения размера кластеров в конфигурациях, приведенных на рис. 7. |
Как видно из графиков, при равном количестве мономеров в кластерах, число свободных связей во фрагментах гексагонального льда по сравнению с таковыми для акванов может быть как больше (более рыхлая структура II), так и меньше (компактный вариант I). Хотя этот факт кажется тривиальным, он подтверждает интуитивную мысль, что вероятность спонтанного образования кластеров по типу льда и по типу акванов примерно одинакова. В такой конкурентной ситуации простейшее решение, которое, по-видимому, может быть предложено, это допустить сосуществование обеих структур через непрерывные осцилляции между ними.
2.5. Осцилляции «порядок-беспорядок»
Прямая трансформация (Ih « Aq) в кластерах размером а = 1-2 нм требует разрыва и повторного замыкания довольно большого числа Н-связей, следовательно, затраты значительной энергии, так что переходы между двумя конфигурациями, вероятно, происходят через их разрушение. При этом локальная плотность меняется от минимального значения, в обоих случаях примерно равного плотности льда, до максимума в момент разупорядочения, который немного выше макроскопической плотности воды. Такая картина согласуется с экспериментом, так как позволяет объяснить рентгеновский контраст, благодаря которому кластеры, как структуры меньшей плотности выделяются на более обширном и плотном фоне [1,2]. Структурные пульсации, раз возникнув, уже не требуют энергетических затрат, так как процесс в целом носит адиабатический характер. Они задают ритм флуктуациям других физических величин, характеризующих макроскопические состояния водных систем и, вероятно, сопряжены с распространением автоволн.
Рост флуктуаций при охлаждении также получает простое объяснение. С уменьшением температуры броуновская диффузия замедляется, что благоприятствует увеличению среднего размера кластеров. Так как в фазе (осцилляций) максимального роста каждый из них состоит из большего числа молекул, и все они участвуют в осцилляциях, то их амплитуда также возрастает. В режиме глубокого переохлаждения форма акванов становится все менее компактной за счет ветвления, и их устойчивость падает. В конечном счете, происходит срыв, называемый однородным зародышеобразованием.
Во Введении упоминался один из нерешенных в работе [1] вопросов о характерном времени существования кластеров t. Вряд ли правильно считать, что структурные пульсации в водном объеме не коррелированны. Скорее всего, верно обратное, и потому существует не какое-то одно характерное время, а иерархия времен. В пользу представления о коллективном характере осцилляций свидетельствуют данные об автоколебаниях люминесценции и орто-пара отношения (см. п. 2.4). Нижняя граница t оценивается нами временем прохождения звуковой волны через область порядка минимального масштаба турбулентной неоднородности (а»1 мм) [45]: tmin~ a/cs ~ 10-6 c. Исходя из данных по т.н. быстрому звуку [46], можно отодвинуть нижний предел еще на 1-2 порядка. В промежуточных временных масштабах, вероятно, имеется период 30-50 с, а верхней границей пока можно считать периодичность 18-19 мин, обнаруженную для автоколебаний (п. 2.4). Ожидается экспериментальное подтверждение (для воды) более длинных периодов, начиная с суточного цикла.
Заключение
Удивительная гармония, наблюдаемая в живой природе, традиционно приписывается специальным свойствам биополимеров, позволяющим гибко адаптироваться к изменениям окружения. Так как живое функционирует в воде, то последней оставляли роль лабильной смазки. В последние десятилетия такое представление начинает меняться. Накапливается все больше фактов о значительном, если не равноправном, вкладе воды в формирование, стабилизацию и целесообразную изменчивость структуры биомолекул. Пришло время поискать внутренний порядок также в воде.
Проблема структуры воды в пределах нескольких координационных сфер возникла давно. Сейчас она приобрела особую актуальность, например, для медицины: активность молекулы лекарственного препарата будет различной в зависимости от того, в какой структурной форме воды эта молекула окажется. Проанализировав имеющиеся и, на наш взгляд, надежные данные, мы приходим к выводу, что решение проблемы может быть ускорено, если обратить внимание не столько на амплитуду, сколько на частотный спектр флуктуаций. Обнаружение в этом спектре скрытых периодичностей будет однозначным свидетельством порядка в структурной динамике. Также интересно использовать простой тест на гистерезис в силе флуктуаций при таянии льда и охлаждении горячей воды.
Предложенная выше качественная модель, в отличие от недоступных для прямой проверки гипотез, физически прозрачна и легко проверяема. В водном объеме происходят непрерывные автоколебания между двумя структурно различными типами кластеров, погруженных в большую по объему, менее организованную и более плотную среду. Одна из структур представляет собой кусочки обычного гексагонального льда, тогда как другая структура принадлежит к классу фракталов, из которых создаются водные каркасы биополимеров, т.е. упорядоченная часть их гидратных оболочек. Энергетические барьеры запрещают непосредственную трансформацию одного типа в другой, поэтому переходы происходят через структурное разупорядочение (ассиметричные переходы «порядок–беспорядок»). Это есть источник термодинамических флуктуаций. С понижением температуры средний размер кластеров увеличивается, и с ним, в согласии с экспериментом, растет амплитуда флуктуаций. Кооперативность взаимодействий, вероятно, приводит к тому, что вода обладает иерархическим набором характерных времен осцилляций, который не зависят от температуры и коррелируют с ритмическими колебаниями относительного содержания орто/пара спин-изомеров Н2О вокруг статистически равновесного отношения 3:1.
Литература
1. C. Huang et al., The inhomogeneous structure of water at ambient conditions. PNAS, 106, 15214–15218 (2009).
2. A. Nilsson, L.G.M. Pettersson. Perspective on the structure of liquid water. Chemical Physics 389, 1–34 (2011).
3. R.J. Speedy, C.A. Angell. Isothermal compressibility of supercooled water and evidence for a thermodynamic singularity at -45°C. J. Chem. Phys., 65, 851-858 (1976).
4. P.H. Pool, F. Sciortino, U. Essmann, H.E. Stanley. Phase behavior of metastable water. Nature, 360, 324-328 (1992).
5. C. A. Angell. Insights into Phases of Liquid Water from Study of Its UnusualGlass- Forming Properties. SCIENCE, 319, 582-587 (2008).
6. Н.А. Бульенков. О возможной роли гидратации как ведущего интеграционного фактора в организации биосистем на различных уровнях их иерархии. Биофизика, 36, 181-242 (1991).
7. P.G. Debenedetti. Metastable liquid: concepts and principles. Princeton U. Press, Princeton, N.Y., 1996.
8. C.A. Angell in Water: A Comprehensive Treatise, Supercooled water, ed Franks F. (Plenum, New York), Vol. 7, 1–81 (2008).
9. Б.Н. Вепринцев. Консервация генетических ресурсов. Ред: Б.Н Вепринцев, Н.Н. Ротт. Пущино, ОНТИ НЦБИ АН СССР, 1980.
10. P.G. Debenedetti, H.E. Stanley. Supercooled and glassy water. Phys. Today, 40-46, June 2003.
11. P. Brűggeller, E. Mayer. Complete vitrification in pure liquid water and dilute aqueous solutions. Nature, 288, 569-571 (1980).
12. O. Mishima, L.D. Calvert, E. Whalley. "Melting ice" I at 77 K and 10 kbar: a new method of making amorphous solids. Nature, 310, 393-395 (1984).
13. O. Mishima. Reversible first-order transition between two H2O amorphs at ca 0.2 GPa and ca. 135 K. J. Chem. Phys. 100, 5910-5912 (1994).
14. O. Mishima, H.E. Stanley. The relationship between liquid, supercooled and glassy water. Nature, 396, 329-335 (1998).
15. C.A. Angell. Amorphous water. Ann. Rev. Phys. Chem, 55, 559-583 (2004).
16. J. Teixeira. The “puzzle” of Water Behavior at Low Temperature. Water. 2, 702-710 (2010).
17. R.J. Speedy. J. Chem. Phys., 86, 982 (1982).
18. Л.Д. Ландау, Е.М. Лифшиц. Статистическая физика. Ч. 1. Гл. 12. М., Наука (1976).
19. K. Stokely, M.G. Mazza, H.E. Stanley, G. Franzese. Effect of hydrogen bond cooperativity on the behavior of water. PNAS, 107, 1301-1306 (2010).
20. M. Beye, F. Sorgenfrei, W. F. Schlotter, W. Wurth, A. Fohlisch. The liquid-liquid phase transition in silicon revealed by snapshots of valence electrons. PNAS, 107, 16772-16776 (2010).
21. В.Г. Бойко, Х.-Й. Могель, В.М. Сысоев, А.В. Чалый. Особенности метастабильных состояний при фазовых переходах жидкость-пар. УФН, 161, 77-111 (1991).
22. Я.И. Френкель. Кинетическая теория жидкости. М. Наука, 1975.
23. J.A. McCammon, S.C. Harvey. Dynamics of proteins and nucleic acids. Cambridge University Press, Cambridge, 1987.
24. R.B. Gregory. Protein-solvent interactions. Marsel Dekker, N.Y., 1995.
25. D.I. Svergun, S. Richard, M.H.J. Koch, Z. Sayers, S. Kuprin, G. Zaccai. Protein hydration in solution: Experimental observation by x-ray and neutron scattering. PNAS, 95, 2267-2272 (1998)].
26. S.K. Pal, A.H. Zewail. Dynamics of Water in Biological Recognition. Chem. Rev., 104, 2099-2123 (2004).
27. N. Niimura, T. Chatake, K. Kurihara, M. Maeda. Hydrogen and hydration in proteins. Cell Biochem. Biophys., 40, 351-369 (2004).
28. Finer-Moore J.S., Kossiakoff A.A., Hurley J.H., Earnest T., Stroud R.M. Solvent structure in crystals of trypsin determined by X-ray and neutron diffraction. Proteins, 12, 203-222 (1992).
29. Kossiakoff A.A., Sintchak M.D., Shpungin J., Presta L.G. Analysis of solvent structure in proteins using neutron D2O-H2O solvent maps: pattern of primary and secondary hydration of trypsin. Proteins, 12, 223-36 (1992).
30. Nakasako M. Large-scale networks of hydration water molecules around proteins investigated by cryogenic X-ray crystallography. Cell Mol Biol., 47, 767-790 (2001).
31. Nakasako M, Fujisa T, Adachi S, Kudo T, Higuchi S. Large-scale domain movements and hydration structure changes in the active-site cleft of unligated glutamate dehydrogenase from Thermococcus profundus studied by cryogenic X-ray crystal structure analysis and small-angle X-ray scattering. Biochemistry, 40, 3069-3079 (2001).
32. ]. Lee J, Kim SH. Water polygons in high-resolution protein crystal structures. Protein Sci., 18, 1370-1376 (2009).
33. В.И. Лобышев, А.Б. Соловей, Н.А. Бульенков. Компьютерный модульный дизайн параметрических структур воды. Биофизика, т. 48, № 6, c 1011-1021 (2003); V.I. Lobyshev, A.B. Solovey, N.A. Bulienkov. Computer construction of modular structures of water. Journal of Molecular Liquids, 106/2-3, pp 277-297 (2003).
34. Г.В. Букин, Е.Б. Вольф, В.П. Данилов, С.Д. Захаров, А.В. Иванов, Т.М. Мурина, Е.Г. Новиков, Н.А. Панасенко, С.Н. Перов, А.М. Прохоров, С.А. Скопинов, М.И. Тимошечкин. Структурные изменения межклеточного раствора, индуцированные прямой генерацией синглетного кислорода в суспензии эритроцитов. Кр.сообщ. по физ., № 1, 18-24 (1991).
35. С.Д. Захаров, А.В. Иванов, Е.Б. Вольф, В.П. Данилов, Т.М. Мурина, К.Т. Нгуен, Е.Г. Новиков, Н.А. Панасенко, С.Н. Перов, С.А. Скопинов, Ю.П. Тимофеев. Структурные перестройки в водной фазе клеточных суспензий и белковых растворов при светокислородном эффекте. Квантовая электроника, 33, 149 - 162 (2003).
36. D.J. Morre, D.M. Morre. ENOX proteins, copper hexahydrate-based ultradian oscillators of the cells’ biological clock. In Ultradian Rhythms from Molecules to Mind, D. Lloyd, E. Rossi (eds.), Springer Science, Business Media B.V., 43-84 (2008).
37. D.J. Morre, J. Orczyk, H. Hignite, C. Kim. Regular oscillatory behavior of aqueous solutions of CuII salts related to effects on equilibrium dynamics of ortho/para hydrogen spin isomers of water. J. Inorg. Biochem., 102, 260-267 (2008).
38. T.I. Quickenden, S.S. Que Hee. The luminescence of water excited by ambient ionizing radiation. Radiat. Res., 46, 28-35 (1971).
39. S.V. Gudkov, V.I. Bruskov, M.E. Astashev, A.V. Chernikov, L.S. Yaguzhinsky, S.D. Zakharov. Oxygen-dependent auto-oscillations of water luminescence triggered by the 1264 nm radiation. J. Phys. Chem. B, 115, 7693–7698 (2011).
40. С.Д. Захаров, И.В. Мосягина. Биофизика (в печати).
41. S. Pershin. Two Liquid Water. Phys. Wave Phenom., 13, 192-208 (2005).
42. Шноль С.Э., Зенченко Т.А., Зенченко К.И., Пожарский Э.В., Коломбет В.А., Кондратов А.А.. Закономерное изменение тонкой структуры статистических распределений как следствие космофизических причин. УФН, 170, 214-218 (2000).
43. C.A. Angell. Insights into phases of liquid water from study of its unusual glass-forming properties. Science, 319, 582-587 (2008).
44. Ш. Ма. Современная теория критических явлений. М., Мир, 1980.
45. М. И. Рабинович, М.М. Сущик. Регулярная и хаотическая динамика структур в течениях жидкости. УФН, 60, 3-64 (1990).
46. G.Ruocco, F.Sette. The history of the “fast sound” in liquid water. Condens. Matter Phys., , 11, 29–46 (2008).